Topics
2023.03.31 circular No.20
乱れを科学する−ゆらぎの研究豊田理化学研究所
西川 惠子
昨年(2022年)秋に、文化功労者に選出された。まさに晴天の霹靂であり、私のような者がその栄誉に浴して良いのかととまどった。今は、地味ではあるが、科学技術を支える縁の下の力持ち的な基礎科学が評価されたことを素直に喜びたいと思っている。
評価の対象は「物質科学におけるゆらぎの研究」であった。イオン液体研究会サーキュラーで、私のライフワークとなった「ゆらぎの研究」を振り返る機会を頂いたことに感謝し、これまでの研究を簡単にご紹介する。
『ゆらぎ』は平均からのズレを表す概念であると私は定義している。空間的な分子分布のズレ(静的ゆらぎ)や時間の情報を含む変動(動的ゆらぎ)は、対象とする系の構造・物性を決め、その後の時間発展の駆動力となる。様々な分野で『ゆらぎ』が注目すべきキーワードとして取り上げられているが、私は以下の3つを、物質科学において『ゆらぎ』が顕在化する系として取り上げてきた。
(1)分子分布の不均一な分布(密度ゆらぎ)・・・超臨界流体
(2) 混合状態(濃度ゆらぎ)・・・溶液、相分離
(3) 動的ゆらぎ・・・相転移
(1)と(2) は静的ゆらぎといえるものであり、(3)は時間情報を持った動的ゆらぎである。(2)については、最近総説を書いたので1, 2)、そちらに譲ることにする。ここでは、主に(1)と(3)について紹介する。
2.分子分布の不均一さ−密度ゆらぎ
分子が不均一に分布している最も良い例は、超臨界流体である。超臨界流体のコンピュータ・シミュレーションによる分子分布(試料:Xe,岡崎進計算)を図1に示した。図示したように、超臨界状態における分子分布は、乱れているとしか言いようがない。この乱れを定量的に表現する発想は皆無であった。動径分布関数で試みようとした研究例もある。しかし、各原子周りの構造の平均化が動径分布関数法の基本であるので、超臨界流体の乱れ構造を平均化することにより、超臨界流体の特質そのものを鈍した情報しか得られない。
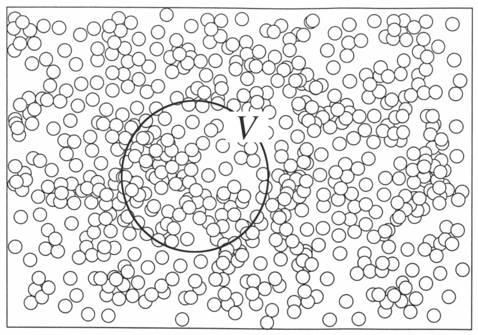
図1 超臨界状態における分子分布。体積V内の粒子数の不均一さを定量化。
超臨界流体の分子分布の不均一さ(図1)を『密度ゆらぎ』表示することを提案した。小角X線散乱強度から密度ゆらぎを求める実験法を確立し、多くの物質(Xe3),CO24),CHF35, 6),CH2F25),C2H47),C6H68),C6H12, CH3OH9),C2H5OH,H2O10, 11)等)の超臨界状態に適用した。研究の観点は、① 温度、圧力あるいは密度を変えた場合、密度ゆらぎはどのように変化するか?;② 物質依存性は?;③ ゆらぎと超臨界流体の物性とどのように関連しているか?を明らかにすることであった。 図2は、密度と温度の2軸に対して超臨界H2Oの密度ゆらぎを描いたものである。密度ゆらぎは、臨界点に近づくにつれ大きな値をとり、臨界点で発散する。等温条件で密度を変えて密度ゆらぎを求めると、ある密度で極大値をとる。様々な温度で求めた極大値を連ねたのが、尾根線である(図2の青の破線)。この尾根線の温度・圧力の相図上への投影が気液曲線の延長線である。当初、この線を『ゆらぎの尾根線』と読んでいたが、最近は、Nishikawa Line(以下N-lineと省略)と呼んでいる。
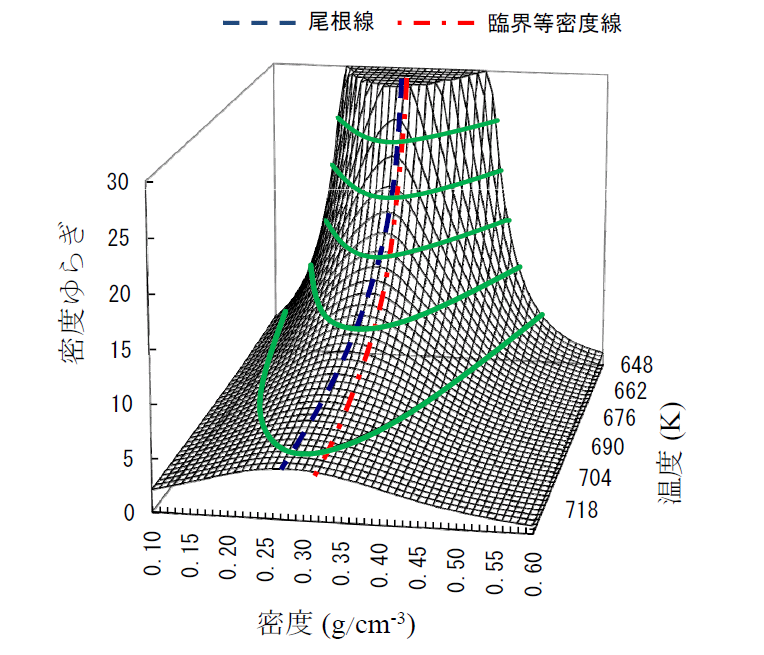
図2 超臨界水の密度ゆらぎ。水の臨界温度: 647 K。 臨界密度: 0.322g/cm3。
多くの物質の密度ゆらぎを求め、ゆらぎが系の性質を決めている重要な物理量であることを明らかにしてきた12, 13)。具体的にまとめると以下の通りである。
a) 密度ゆらぎの等高線を温度・圧力の相図に描くと、気液曲線を延長する形でN-lineが存在する。
b) N-lineは、臨界点を除いて臨界等密度線とは一致せず、臨界点から離れるに従いそのずれは大きくなる。 (図2の破線と一点鎖線)
c) N-line上で、G(Gibbs energy)の2次微分量に関連した物理量は極値をとる。(例えば、比熱、等温圧縮率、膨張率、音速、熱伝導率など)。
d) 溶解度の変化率は、N-line上で最大になる。すなわちN-lineを境として非常に溶解度の大きな領域と溶解度の小さな領域に分かれる。
e) 超臨界流体を媒体として反応を行った場合、反応の特異点はN-line上にあることが多い。より正確に表現すると、Gの2次微分量が反応の律速段階を決めている場合、N-line上が反応の特異点となる。
f) すべての物質でa)〜e)は成立する。臨界定数で規格化すると、水素結合系と非水素結合系で尾根線の位置に多少ずれがあるものの、N-lineはほとんど重なる(物質に依存しない普遍的性質の発見)。
上述した事実は、N-lineは超臨界領域における何らかの境界線であることを暗示している。尾根線の物理的な意味づけを明らかにするため、van der Waals 状態方程式を用いて密度ゆらぎの尾根線を解析的に式で表してみた14)。物理的な意味を考察した結果、尾根線はGのすべての2次の微分量が極値となる点の軌跡であり、数学的にも臨界点で気液共存線と滑らかに繋がっていることが明らかになった。
横軸に温度、縦軸に圧力で表示した通常の相図では、気液曲線は臨界点でプツリと途切れている。しかし、以上の結果を相図の観点からまとめると、実は、「気液曲線を延長する形で、超臨界流体領域に名残の境界線が続いている。」と結論した。その名残の線が、N-lineである。相図に描かれる各相の境界線は1次の相転移線である。それと対比させるならば、N-lineは高次の相転移線とも表現できるかもしれない。
気液共存線が臨界点で途切れ、超臨界領域では何もその影響が無いというのは不自然である。N-lineは、超臨界領域における気液共存線の名残であり、『より気体的な領域』と『より液体的な領域』の境界線と言える。c)〜e)に示すようにN-line近辺は超臨界流体の特異性が最も顕著に出る領域であり超臨界流体を機能場として用いる際に重要な場となる。このように、ゆらぎが超臨界流体の特異的物性を決めていることを明らかにした。
液体と同様、溶液構造を表現する方法は動径分布関数法が一般的である。動径分布関数は、液体あるいは溶液中の一原子の上に乗り(中心原子と定義)、その周りに他の原子がどのように分布しているのかを示す関数である。そして、中心原子を次々に変えて得られる分布関数を平均化したものである。
動径分布関数は、中心原子から第1〜第2近接分子までの構造情報である。単原子液体などでは意味があるが、複雑な系では動径分布関数の解釈は困難になり、得られる情報は非常に少なくなる。結晶構造との対応で議論することが多く、乱れた系を無理に規則構造で理解しようとする考え方と言える。また、クラスタリングやミクロな相分離が起こっている系では、着目領域として数nm〜数10 nmの構造を観測する必要があるが、動径分布関数法ではそれ等の情報を引き出せない。この大きさの空間領域は、“失われた領域”とも呼ばれ、複雑凝集系では、最も構造情報が得にくいメゾスケール領域である。動径分布関数に替わり、メゾスケールで混ざり具合を表現する方法として、濃度ゆらぎを考えた。詳細は最近まとめた総説を参照願いたい1, 2) 。
動的ゆらぎが観測できる系は、相転移現象が最適であると位置づけた。通常、相転移はAvogadro数個程度の粒子の協奏現象であり、通常の物質ではマイクロ秒〜ミリ秒の時間スケールで起こる。イオン液体を試料とした場合、相転移は比較的ゆっくり起こり、観測し易い。我々は、手造りの超高感度熱測定で相転移時の熱の出入りとして、また、NMRの緩和時間測定でイオン液体の相変化のダイナミクスを追ってきた。ここでは、最近まとまったNMR測定の結果を多少詳しく報告する。
4.1 はじめに
柔粘性イオン性結晶(IPC)は、イオンの配向秩序は融解しているが重心は秩序化しているイオン性物質の相と定義される。通常、球形に近いイオンが激しく回転しているか、配向が大きく乱れている。当初、物理化学者や物性研究者が、構成粒子が分子である柔粘性結晶(PC)を液体と通常の結晶の中間状態として注目し、 多くの基礎的な研究を行ってきた 15, 16)。 最近では、PC相を持つイオン液体(IL)が多数発見されている。これらはIPCとして、特に電解質の材料科学から注目され、MacFarlane のグループを中心に活発に研究が進められている17-23) 。「ゆらぎの研究」の立場からは、PC相では構成イオンが活発な動きをしていることが予想され、動的ゆらぎを調べるのに格好の試料と言える。
回折実験から得られるIPCの静的構造は既報論文24 , 25)に譲り、ここでは動的挙動に注目する。イオン液体の動的挙動は、比較的遅いダイナミクスが支配的である。NMR分光法は、物質の再配向ダイナミクスを調べるのに適した方法である。特に、縦緩和時間や横緩和時間(T1,T2)は、比較的遅いダイナミクスが支配的である粘性液体やガラス状固体の物質のダイナミクスや分子間相互作用に関する貴重な情報を与えてくれることが多い26)。これまでも、1H, 19F, 13C のNMRで、分子の再配向ダイナミクスや並進拡散が調べられているが、T1, T2 データを用いてイオン液体の相転移を論じた報告はほとんどない。これに対し、我々のグループでは、主に1HのT1, T2を測定することにより、いくつかのイオン液体の液体と結晶の間の相転移時のダイナミクスを研究してきた27-33) 。
本研究では、液体相、PC相、結晶相の間の相転移ダイナミクスに注目するために、PC相を持つILを試料として選択した。N-butyl-N-methylpiperidinium hexafluorophosphate ([C1C4pip]PF6,図3) は、 ILとしてはあまりポピュラーな試料ではないが、PC相を持つILやILのプロトタイプの多くが融点以前もしくは融点で分解してしまうのに対し、液相を持つ試料である。この点で、系統的に相転移を調べるのに適している。 T1 と T2 はそれぞれ主に回転運動と並進運動を反映しているため、それぞれのダイナミクスに関する情報を個別に得ることができる。また、水素原子とフッ素原子はそれぞれ陽イオン[C1C4pip]+と陰イオンPF6− にのみ含まれているので、1Hと19F緩和時間の測定により、陽イオンと陰イオンのダイナミクスに関する情報を別々に得ることができる。
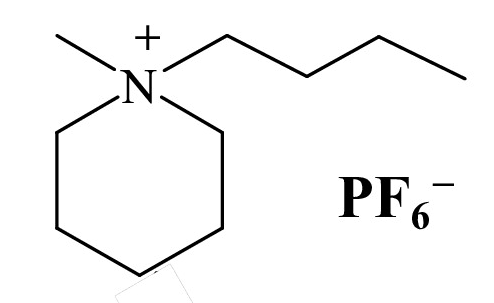
図3 [C1C4pip]PF6の構造。
4.2 結果と議論
4.2.1 相変化
本題のNMR実験結果を理解するために、まず DSC の結果に基づいて [C1C4pip]PF6の相挙動について概説する。試料を370Kまで加熱すると、完全に融解した。図4 は 190~370 K の DSC 軌跡であり、冷却過程では 349 K と 287 K に、昇温過程では 324 K と 354 K にそれぞれ 2 つの発熱ピークと 2 つの吸熱ピークが観測された。この結果から、[C1C4pip]PF6は高温側からPhase IとPhase IIという2つの結晶相を持つことがわかった。一般にイオン液体は過冷却相変化を起こしやすく、冷却過程での変化の温度は実験条件によって異なる。そのため昇温過程のデータがより本質的であり、融点は354K、Phase IIからPhase Iへの相転移温度は324Kであると決定される。以後、昇温過程での現象を議論する。
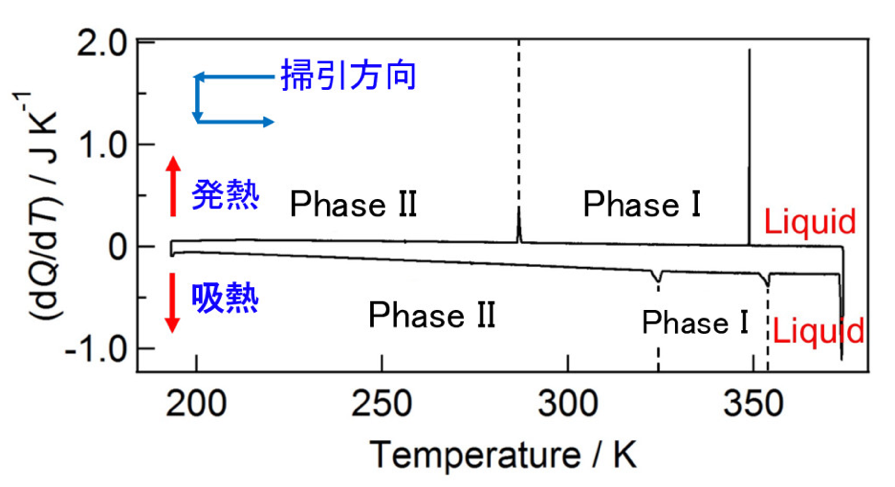
図4 [C1C4pip]PF6の示差走査熱量(DSC)曲線。試料は5 mK/sの掃引速度で370 Kから190Kまで冷却、その後370K まで昇温。
[C1C4pip]PF6の粉末X線回折パターンの解析で、Phase Iは逆NiAs型構造のIPC相、Phase IIは通常の規則結晶であることを明らかにした。さらに、構成イオンの対称性とイオンの位置するサイトから要請される対称性の詳細な考察から、Phase Iについては、[C1C4pip]+ は少なくとも2軸の周りを自由に回転している必要があり、対称性の高いPF6-は平衡位置の周りを自由に回転または秤動運動していると結論付けた25)。
4.2.2 水素核のT1とT2
1H 共鳴周波数 25 MHz、19F 共鳴周波数 23.52 MHz のパルス NMR 装置(いずれもJEOL製)を用いた。低い共鳴周波数を選択しているため、化学シフトによる信号の分離が小さく、[C1C4pip]+イオン中のH原子とPF6-イオン中のF原子の全体的なダイナミクスを観測している。T1測定は反転回復法を用い、T2の測定では、液相はCurr-Purcell-Meiboom-Gill (CPMG)法を、PC結晶相と結晶相はSolid echo法を用いた34) 。
プロトン間の双極子緩和機構では、T1 と T2 は次のように記述できる。
![]() (1)
(1)
および
![]() , (2)
, (2)
ここにγは磁気回転比、ℏはディラック定数、rはプロトン間距離、τcは相関時間である34, 35)。 スペクトル密度関数J(ω)は次のように記述される。
J(ω) = τc /(1+ω2τc 2). (3)
粘性液体の 1H-T1 と T2 の温度依存性の典型例として、グリセリンの挙動を図5 に示す。1/T2値はτcと正の相関のため、T2は単純に温度が下がると減少する。1/T1は、ωτc << 1の領域(極端先鋭化条件)ではτcに、ωτc >> 1の領域では1/τcに比例する。その結果、一相内でのT1 vs. 温度の曲線は、グリセリンの例で示されるように、高温領域では正、低温領域では負の傾きを持ち、極小値はωτc = 0.62である35)。相転移を持つ試料では、各相転移温度でT1,T2 値の不連続な変化が観測される。
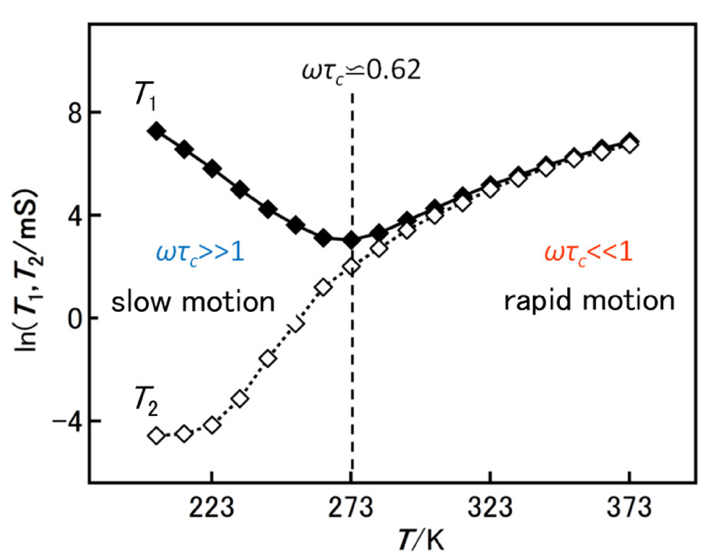
図5 グリセリンの1H-T1と1H-T2の温度変化。
粘性液体では、一般に双極子-双極子緩和機構が支配的である。この機構では、図5 に示すように、高温領域(すなわちωτc << 1の領域)においてT1とT2の値はかなりよく一致し、次のように表される。
![]() (4)
(4)
また、双極子-双極子緩和では、分子の再配向運動と分子内運動がT1の値に寄与する主要な運動であり、並進運動は主にT2の値に寄与する34)。
まず、1H-T1 の挙動に注目する。H原子は陽イオン [C1C4pip]+にのみ含まれるため、1Hの情報は陽イオンのダイナミクスに関係するものである。図6 に、[C1C4pip]+ のT1(開いた赤丸)とT2(閉じた赤丸)の振る舞いの温度依存性(加熱過程)を示す。
まず、1H-T1 の温度依存性について述べる(図6参照)。T1 の曲線は324Kでわずかに不連続な変化が見られ、これは Phase II→ Phase I の転移に相当するが、Phase I →液相の曲線は354Kで滑らかにつながっている。これは Phase II と Phase I の間に回転運動の差があり、Phase I と液相の間には無いことを示唆している。一般にIPCでは、イオンの重心は規則正しい格子を形成しているが、その配向が乱れていたり、イオンが回転運動しているとされている。粉末結晶X線回折データの構造解析で明らかにしたように、Phase I は IPC相であり、[C1C4pip]+ イオンは少なくとも2軸の周りを回転運動している25)。 Phase I ↔液体状態の相転移点での1H-T1曲線が滑らかに繋がることから、Phase Iでの[C1C4pip]+イオンの回転ダイナミクスは液体状態と同じであると結論される。Phase II は通常の規則正しい結晶である25)。Phase I と Phase II の相転移におけるT1 曲線の不連続な変化は、それぞれの相におけるイオンの回転ダイナミクスの違いを反映している。Phase II では陽イオンはもはや完全に自由に回転することができないと考えられる。
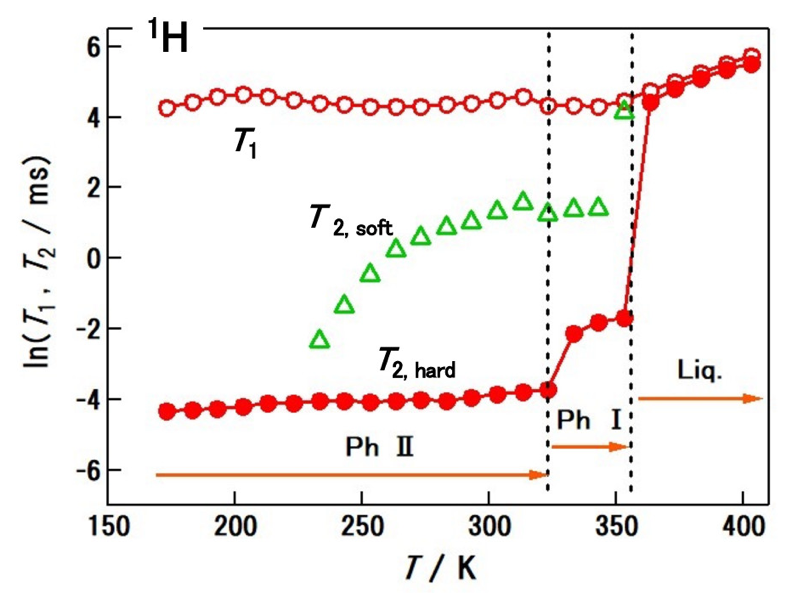
図6 [C1C4pip]PF6の1HのT1(開いた赤丸)とT2(閉じた赤丸)。縦軸は対数スケール。緑の三角は、Phase II およびPhase Iに現れた柔らかい成分のT2。
次に、1H-T2の挙動に注目する。T2の温度依存性は図6の閉じた赤丸で示した通りである。T2を決定する際、自由誘導減衰(FID)信号を注意深く観察したところ、硬い成分(FIDの速い減衰、T2が小)と柔らかい成分(FIDの遅い減衰、T2が大)の二つの緩和機構が存在することが判明した。硬い成分のT2値は結晶のT2値に対応し、図6の閉じた赤丸で示されている。柔らかい成分のT2値は緑色の三角形で示した。19FのT2にも同様の現象が見られるので、1Hと19Fの柔らかい成分の緩和機構については、後の4. 2. 4 節で議論する。
T2 は全領域で 1/τc と正の相関があり、並進運動がその値に反映される。Phase II → Phase I→液体の各相転移点では、T2の値は不連続に変化し、並進運動の形態が各相で異なっていることがわかる。[C1C4pip]PF6のPhase IIにおけるT2の値は、イオン液体の通常の結晶相である他の塩の値とほぼ同じ大きさである。これは、[C1C4pip]+イオンの並進運動がPhase IIで概ね固定化されていることを示している。 Phase I(IPC相)では、液相ほどではないものの、かなり大きな並進運動が存在することが示された。一般にIPC相では、イオンは格子点を飛び越えるような運動をすると予想される。このT2のデータは、この予想を裏付けている。
19Fの核スピンは1/2なので、1Hで用いた式(式(1)-式(4))がそのまま適用される。図7では、19FのT1,T2の温度依存性をそれぞれ開いた赤丸、閉じた赤丸で示した。フッ素原子は陰イオンのみに含まれるため、T1は主に陰イオンの回転運動の温度依存性を、T2は主に並進運動の温度依存性を示している。
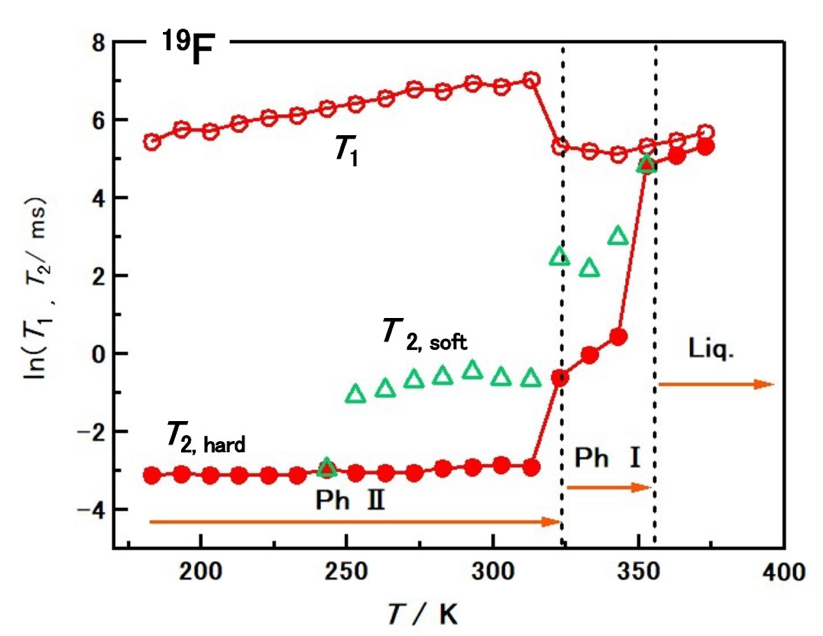
図7 [C1C4pip]PF6の19FのT1(開いた赤丸)とT2(閉じた赤丸)。縦軸は対数スケール。緑の三角は、Phase II およびPhase Iに現れた柔らかい成分のT2。
まず、T1の温度依存性に注目する。陽イオン(1Hデータ)の場合と同様に、phase I → 液相の転移点において曲線が滑らかにつながっている。つまり、陰イオンは IPC相 (phase I) と液相で同様の自由回転運動をしていることが予想される。phase II →phase I の転移点で、T1の不連続な変化を考慮すると、phase IIのPF6-イオンは異なる回転運動様式になると想像され、その運動様式は平衡位置を中心とした秤動的な運動と予想される。陰イオンの回転運動は、平衡点での全体的な回転運動と秤動的な運動の2種類しかない。この運動モードの切り替えは、phase II →phase I の相転移点で起こる。1H- T1とは異なり、Phase IIにおける19F-T1の変化は温度の上昇に伴い単調に増加する。これは、この領域では陰イオンの回転モードが1つだけ存在することを示している。
図7 の19F-T2 (赤の閉じた円) は、1H-T2と同様に、各相転移点での不連続な変化を示している。このことから、陰イオンの並進運動の形態は相ごとに異なり、高温相でより活発であると結論される。
相転移のダイナミクスを別の角度から調べるために、パルスNMRの自由誘導減衰(FID)信号について調べた。FID 信号とは、励起パルスを印加した直後に現れる磁化の横方向成分である。
励起パルスをx軸方向に印加すると、t = 0での横磁化M(0)=M0 がy軸方向に現れる。M0はz軸方向の平衡磁化であり、磁化は時間の経過とともにゼロの平衡状態まで減衰していく。t秒後のy軸方向の磁化、M(t)は次のように表される34)。
M(t) = M0 exp(-t/T2). (5)
1H-T2 と 19F-T2 の測定では、どちらの FID 信号も 2 つの成分から構成されている。横緩和時間が、硬いT2と柔らかいT2の2成分からなる場合、FID 信号は以下のように表される。
M(t) = (1- x) M0 exp(-t/T2, hard) + x M0 exp(-t/T2, soft), (6)
ここに x は柔らかい成分の比率である。減衰の速い信号が硬い成分、遅い信号が柔らかい成分に相当する。
図6では、1H-T2の硬い成分と柔らかい成分の値を、それぞれ赤の閉じた丸と緑の開いた三角で示した。また、19F-T2のハード成分とソフト成分の値を、1H- T2と同じ記号で図7に示した。1H,19Fともに、液体状態では M(t) 信号の成分は1つだけである。融点では、Phase Iの1Hと19Fの両方の柔らかい成分が、液体状態で赤い閉じた円で示されたそれぞれの成分につながっている。
今回の試料[C1C4pip]PF6では、温度の上昇とともに柔らかい成分(T2が大)が増加する現象が見られる。1H-T2に関しては、柔らかい成分の比率(x)の温度依存性を図8に示した。柔らかい成分が自由な並進運動を特徴とする液体状の成分を、硬い成分が通常の結晶を示している。これは、硬い成分の T2 値がこれまで測定したイオン液体の秩序結晶の T2 値と同じオーダーであること、 および柔らかい成分の T2 値が融点における液体の T2 と滑らかにつながっていることからも結論付けられる。
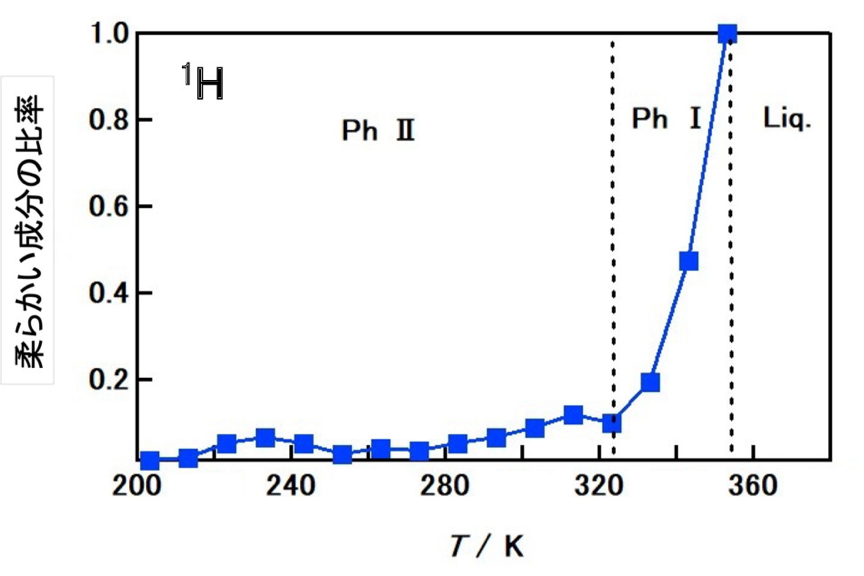
図8 1H-T2における柔らかい成分の割合。
図8に示すように、柔らかい成分は通常の結晶状態(Phase II)で既に存在し、Phase Iへの相転移に向けてゆっくりと増加するが、その割合は数%以下である。Phase Iでは、温度の上昇とともに比率が急激に増加し、融点で1.0に達し、液体状態となる。Phase IIにおける比率曲線のうねりは意味がなく、比率の値が非常に小さいために起こる解析誤差であると考えられる。 図6、図7のソフト成分の値(緑の三角形)に着目してみよう。240K以下では存在比が低いが、結晶領域でもphase Iまで徐々に増加する。phase Iの柔らかい成分は結晶中のT2 値と液体中のT2 値の中間である。T2 値は主に目的元素を含む各イオンの並進運動が反映されている。以上をまとめると、ソフト成分の出現は、陽イオンと陰イオンがそれぞれ単独ではなく、共同して起こるダイナミックな現象であると考えられる。その現象の可能性としては、結晶の表面や界面で起こる表面融解や界面融解が考えられる。イオン液体の結晶状態において、表面または界面融解が起こりやすいことは既に報告した36)。 結晶の表面または界面において、一部の陰イオンと陽イオンは対になって融解し並進運動を開始するが、この運動は通常の液体における運動よりも自由度が低いと予想される。今回の1H-T2 の2 つの成分の存在は、並進運動の前駆融解現象を捉えているものと思われる。
4.2.5 活性化エネルギー
相関時間 tc は、Arrhenius方程式に従う。
tc = ta exp (Ea/RT), (7)
ここで、Eaは活性化エネルギーである。tcは緩和率1/T1 に比例するので、tcw >> 1 の条件を満たす温度領域では、対応する運動のEaを見積もることができる。
[C1C4pip]+の回転運動を反映する1Hデータについては、T1測定を行った2つの温度領域を選択した。一つは353−393Kの領域で、ここからEa=30 kJ/molが得られた。この値は、液相での陽イオンの回転運動全体の活性化エネルギーに相当すると思われる。もう一つは173−183Kの温度領域で、ここからEa=4.9 kJ/molが得られた。このエネルギーは、メチル基の回転活性化エネルギーに対応すると思われる。中間領域では、いくつかのモードの寄与が重なっている。この温度領域でのT1挙動を特徴づける候補は、ブチル基の部分運動とピペリジニウム環の環運動であると考えられるが、その活性化エネルギーは推定できない。
PF6-の回転運動を反映する19F−T1に関しては、2種類の回転モードに対する活性化エネルギーを得ることができる。一つは347−373Kの領域で18.9 kJ/molであり、この値は液体状態のPF6の自由回転の活性化エネルギーに対応するものであろう。もう一つは、183−313Kの領域から5.8 kJ/molである。この値は、秩序結晶相におけるPF6-の平衡位置の周りの秤動運動の活性化エネルギーに対応すると考えられる。PF6-の運動のモードは単純であるため、モードの割り当てと活性化エネルギーの決定が可能である。
以上のように、PC相を持つ試料では、PC相はもちろん、結晶相でも活発なイオン移動が見られる。それらを捉えるには、NMR緩和時間測定が最適であると結論づけられる。
また、ILはその高粘性のため、遅いダイナミクスで特徴づけられる。この点からも、ILは相転移現象を研究するのにうってつけの試料と言える。
なお、NMRによる [C1C4pip]PF6 の動的ゆらぎの研究は、投稿中の論文37)を簡単にまとめ直し、解説したものである。
文献
- K. Nishikawa, Bull. Chem. Soc. Jpn., 94 (2021) 2170.
- 西川惠子,日本結晶学会誌, 63 (2021) 197.
- Y. Tanaka, Y. Takahashi, T. Morita, K. Nishikawa, Jpn. J. Appl. Phys. 47 (2008) 334.
- K. Nishikawa, I. Tanaka, Y. Amemiya, J. Phys. Chem. 100 (1996) 418.
- T. Morita, Y. Takahashi, Y. Tanaka, A. A. Arai, K. Nishikawa J. Chem. Phys. 124 (2006)124549.
- K. Saitow, D. Kajiya, K. Nishikawa, J. Am. Chem. Soc., 126 (2004) 422.
- K. Nishikawa, H. Ochiai, K. Saitow, T. Morita, Chem. Phys. 286 (2003) 421.
- A. A. Arai, T. Morita, K. Nishikawa, J. Chem. Phys. 119 (2003) 1502.
- T. Morita, T. Kadota, K. Kusano, Y. Tanaka, K. Nishikawa, Jpn. J. Appl. Phys. 62 (2023) 016504.
- T. Morita, K. Kusano, H. Ochiai, K. Saitow, K. Nishikawa, J. Chem. Phys. 112 (2000) 4203.
- N. Yoshida, M. Matsugami, Y. Hirano, K. Nishikawa, F. Hirata, J, 4 (2021) 698.
- K. Nishikawa, T. Morita, J. Supercritical Fluids 13 (1998) 143.
- K. Nishikawa, T. Morita, Chem. Phys. Lett. 316 (2000) 238.
- K. Nishikawa, K. Kusano, A. A. Arai, T. Morita, J. Chem. Phys. 118 (2003) 1341.
- J. Timmermans, J. Phys. Chem. Solids 18 (1961) 1.
- 関集三, 化学と工業, 15 (1962) 1226 and referenced cited therein.
- D. R. MacFarlane, J. Huang, M. Forsyth, Nature, 402 (1999) 792.
- D. R. MacFarlane, M. Forsyth, Adv. Mater., 13 (2001) 957.
- J. M. Pringle, P. C. Howlett, D. R. MacFarlane, M. Forsyth J. Mater. Chem., 20 (2010) 2056.
- H. Zhu, D. R. MacFarlane, J. M. Pringle, M. Forsyth, Trends Chem., 1 (2019) 126.
- J. Hwang, K. Matsumoto, C. –Y. Chen, R. Hagiwara, Energy Environ. Sci., 14 (2021) 5834.
- H. Yamada, Y. Miyachi, Y. Takeoka, M. Rikukawa, M. Yoshizawa-Fujita, Electrochim. Acta, 303 (2019) 293.
- D. Al-Masri, R. Yunis, A. F. Hollenkamp, J. M. Pringle, ChemElectroChem, 7 (2020) 4118.
- K. Nishikawa, T. Yamada, K. Fujii, H. Masu, K. Tozaki, T. Endo, Bull. Chem. Soc. Jpn., 94
(2021) 2003.
- K. Nishikawa K. Fujii, T. Yamada, M. Yoshizawa-Fujita, K. Matsumoto, Chem. Phys. Lett. 803 (2022) 139771.
- C. A. Angell, Chem. Rev. 90 (1990) 523.
- M. Imanari, K. Uchida, K. Miyano, H. Seki, K. Nishikawa, Phys. Chem. Chem. Phys 12
(2010) 2959.
- T. Endo, S. Widgeon, P. Yu, S. Sen , K. Nishikawa, Phys. Rev. B, 85 (2012) 054307.
- T. Endo, H. Murata, M. Imanari, N. Mizushima, H. Seki, K. Nishikawa, J. Phys. Chem. B, 116 (2012) 3780.
- M. Imanari, K. Fujii, T. Endo, H. Seki, K. Tozaki, K. Nishikawa, J. Phys. Chem. B, 116 (2012) 3991.
- T. Endo, H. Murata, M. Imanari, N. Mizhisima, H. Seki, S. Sen, K. Nishikawa, J. Phys. Chem. B, 117 (2013) 326.
- M. Imanari, K. Fujii, T. Mukai, N. Mizushima, H. Seki, K. Nishikawa Phys. Chem. Chem. Phys., 17 (2015) 8750.
- Y. Shimizu, Y. Wachi, K. Fujii, M. Imanari, K. Nishikawa, J. Phys. Chem. B, 120 (2016) 5710.
- T. C. Farrar, E. D. Becker, Pulse and Fourier Transform NMR, Introduction to Theory and Method, Academic Press, New York 1971.
- I. Solomon Phys. Rev., 99 (1955) 559.
- K. Nishikawa, K. Fujii, Y. Hashimoto, K. Tozaki, Phys. Chem. Chem. Phys., 22 (2020) 20634.
- K. Nishikawa, K. Fujii, Phys. Chem. Chem. Phys., submitted.
